|
3 Существует множество моделей распространения звука в пористых средах [12-21]. Нас интересует, как будет зависеть скорость звука в твердом теле с воздушными порами от их концентрации. Так, для металлов при пористости менее 20% такая зависимость имеет вид [21]:
где 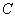 - скорость звука в пористом образце, - скорость звука в пористом образце, 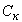 - скорость звука в твердой фазе образца металла (т.е. в отсутствие пор), P - объемная пористость образца. - скорость звука в твердой фазе образца металла (т.е. в отсутствие пор), P - объемная пористость образца.
Определим скорость звука в композите в отсутствие пор как скорость звука в двухфазной среде. Пусть в образце композита с нулевой пористостью и объемом V0 содержание матрицы будет
где 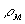 - плотность вещества матрицы, - плотность вещества матрицы, 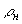 - плотность вещества наполнителя. - плотность вещества наполнителя.
Пусть на исследуемый образец c нулевой пористостью падает акустическая волна с плоским волновым фронтом. Скорость звуковой волны С0 в этом образце можно выразить через приращение акустического давления и плотности этого слоя [22]:
Аналогично для скорости звука в обеих фазах – в матрице и в наполнителе:
Запишем выражения для плотности вещества и выразим ее через приращение объема этого вещества:
где 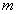 - масса вещества, - масса вещества,  - объем вещества. - объем вещества.
Применительно к образцу композита имеем:
где 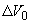 - приращение объема всего образца, - приращение объема всего образца, 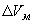 - приращение объема матрицы в образце, - приращение объема матрицы в образце, 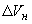 - приращение объема наполнителя в образце. - приращение объема наполнителя в образце.
Подставим (10) в (11) и получим:
Учитывая, что 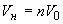 , и , и 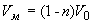 получаем выражение для приращения плотности двухфазной среды: получаем выражение для приращения плотности двухфазной среды:
Отсюда с учетом (7) и (8) получим выражение для скорости звука в двухфазной среде:
или
Окончательно, с учетом (5 ) и (6), получим для скорости звука в пористом композите:
Выразим пористость через скорость звука из (15):
С помощью (16) мы получаем возможность определять пористость участка исследуемого образца графито-эпоксидного композита, измеряя фазовую скорость звука в этом участке.
|
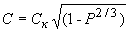 (5)
(5)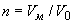 , где
, где 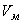 - объем, занимаемый в образце матрицей. Тогда
- объем, занимаемый в образце матрицей. Тогда 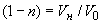 - объемное содержание наполнителя в образце с нулевой пористостью, где
- объемное содержание наполнителя в образце с нулевой пористостью, где 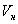 - объем, занимаемый наполнителем. Плотность двухфазной среды (композита без пор):
- объем, занимаемый наполнителем. Плотность двухфазной среды (композита без пор):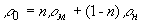 (6)
(6)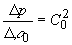 (7)
(7)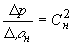 (8)
(8)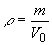 (9)
(9)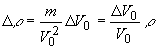 (10)
(10)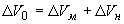 (11)
(11)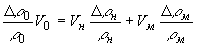 (12)
(12) (13)
(13)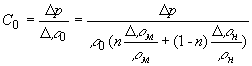
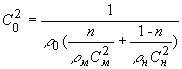 (14)
(14)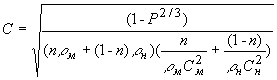 (15)
(15)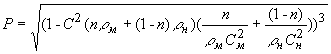 (16)
(16)