3. Теоретический расчет пространственного распределения интенсивности света в условиях многократного рассеяния.
Решение задачи об импульсном лазерном возбуждении звука разбивается на три этапа:
(а) - расчет плотности тепловыделения в рассеивающей среде.
(б) - расчет теплового поля, создаваемого найденными на первом этапе источниками тепла.
(в) - нахождение акустического поля в среде, излучаемого рассчитанными выше тепловыми полями.
Каждая из этих задач не имеет в общем случае аналитического решения. Поэтому анализ термооптического возбуждения звука в рассеивающей среде возможен только при дополнительных упрощающих предположениях.
Рассмотрим полубесконечную среду с коэффициентами поглощения и рассеяния света ma и ms соответственно, занимающую полупространство z>0. В случае, если рассеяние преобладает над поглощением ( ), в среде реализуется режим многократного рассеяния излучения [40]. При падении на такую среду светового импульса с плоским волновым фронтом (интенсивность падающего лазерного излучения ), в среде реализуется режим многократного рассеяния излучения [40]. При падении на такую среду светового импульса с плоским волновым фронтом (интенсивность падающего лазерного излучения 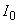 , характерная длительность импульса , характерная длительность импульса 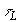 ) интенсивность излучения внутри среды может быть представлена как сумма ослабленного первичного пучка фотонов, еще не претерпевших рассеяния, ) интенсивность излучения внутри среды может быть представлена как сумма ослабленного первичного пучка фотонов, еще не претерпевших рассеяния, 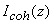 и диффузного поля рассеянного света и диффузного поля рассеянного света 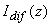 . Первая из этих составляющих быстро спадает с увеличением z [41]: . Первая из этих составляющих быстро спадает с увеличением z [41]:
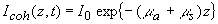 (3.1) (3.1)
а вторая может быть найдена в диффузионном приближении (см., например, [38,39]):
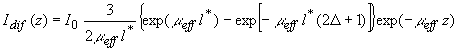 (3.2) (3.2)
где 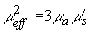 - квадрат коэффициента экстинкции света - квадрат коэффициента экстинкции света; 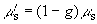 - приведенный коэффициент рассеяния света, - приведенный коэффициент рассеяния света, 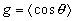 - средний косинус угла однократного рассеяния q - средний косинус угла однократного рассеяния q; 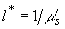 - средняя транспортная длина свободного пробега фотона, т. е. среднее расстояние, которое проходит фотон в среде без изменения своей траектории; - средняя транспортная длина свободного пробега фотона, т. е. среднее расстояние, которое проходит фотон в среде без изменения своей траектории; 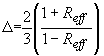 - постоянная, зависящая от соотношения показателей преломления прозрачной и рассеивающей сред, - постоянная, зависящая от соотношения показателей преломления прозрачной и рассеивающей сред, 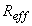 - эффективный коэффициент отражения диффузного излучения от границы раздела. Известно - эффективный коэффициент отражения диффузного излучения от границы раздела. Известно [41,42,43] , что диффузионное приближение достаточно хорошо описывает функцию 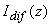 вдали от границы рассеивающей среды и источников излучения (при вдали от границы рассеивающей среды и источников излучения (при 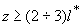 ). Следовательно, интенсивность света внутри рассеивающей среды на расстояниях ). Следовательно, интенсивность света внутри рассеивающей среды на расстояниях 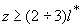 :
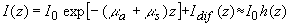 (3.3) (3.3)
где функция
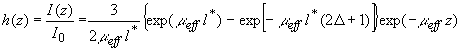 (3.4) (3.4)
описывает пространственное распределение интенсивности света в диффузионном приближении и на расстояниях 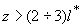 определяется только диффузной компонентой рассеянного светового поля (второе слагаемое в (3.3)), поскольку в приближении определяется только диффузной компонентой рассеянного светового поля (второе слагаемое в (3.3)), поскольку в приближении  коэффициент экстинкции света коэффициент экстинкции света 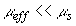 .
В общем случае интенсивность света в рассеивающей среде представляется в виде 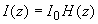 , однако в области , однако в области 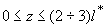 аналитическое выражение для пространственного распределения интенсивности света в среде H аналитическое выражение для пространственного распределения интенсивности света в среде H( z) , полученное в рамках диффузионной теории, неправильно описывает реальную функцию H( z) в исследуемой среде (см., например, [14,21,44]) . Поэтому для расчета пространственного распределения интенсивности света в исследуемой среде на расстояниях 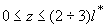 необходимо решить уравнение переноса излучения необходимо решить уравнение переноса излучения [40]:
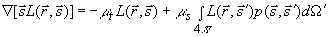 (3.5) (3.5)
где 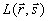 - угловой спектр интенсивности, т. е. интенсивность света в точке - угловой спектр интенсивности, т. е. интенсивность света в точке 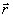 в направлении в направлении 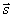 , 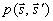 - фазовая функция, - фазовая функция, 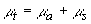 - полный коэффициент ослабления света в рассеивающей среде, - полный коэффициент ослабления света в рассеивающей среде, 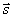 и и 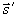 - единичные векторы в направлении рапространения падающего и рассеянного фотонов (см. рис.1), - единичные векторы в направлении рапространения падающего и рассеянного фотонов (см. рис.1),  - единичный телесный угол. В качестве - единичный телесный угол. В качестве
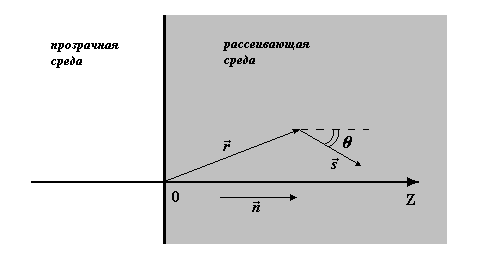
Рис.1: Пояснение к уравнению переноса излучения.
фазовой функции 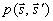 для случаев сильной анизотропии рассеяния обычно используют фазовую функцию Хеньи - Гринштейна для случаев сильной анизотропии рассеяния обычно используют фазовую функцию Хеньи - Гринштейна [45]:
 (3.6) (3.6)
При падении на исследуемую рассеивающую среду светового импульса с плоским волновым фронтом уравнение (3.5) может быть преобразовано к виду:
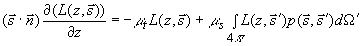 (3.7) (3.7)
где 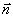 - единичный вектор в направлении оси - единичный вектор в направлении оси 0z . Интенсивность света в исследуемой сильнорассеивающей среде 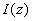 в точке в точке 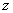 связана с лучевой интенсивностью связана с лучевой интенсивностью 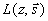 следующим соотношением следующим соотношением [40]:
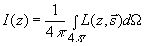 (3.8) (3.8)
Таким образом, решив интегродифференциальное уравнение (3.7), можно затем, используя формулу (3.8), рассчитать интенсивность света 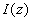 в любой точке исследуемой среды. в любой точке исследуемой среды.
Для решения уравнения (3.7) представим лучевую интенсивность света 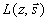 внутри среды в виде суммы двух составляющих внутри среды в виде суммы двух составляющих [40] : когерентной 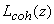 и диффузной и диффузной 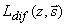 . В результате из уравнения (3.7) получим: . В результате из уравнения (3.7) получим:
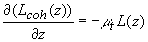 (3.9а) (3.9а)
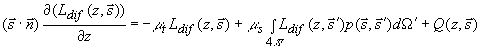 (3.9б) (3.9б)
где 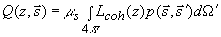 - функция источника для поля рассеяного света. Когерентная составляющая лучевой интенсивности - функция источника для поля рассеяного света. Когерентная составляющая лучевой интенсивности 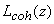 может быть легко найдена как решение уравнения (3.9а). Для решения уравнения (3.9б) его необходимо дополнить граничным условием. Граничное условие переизлучения [21] устанавливает соотношение между диффузным светом, направленным вглубь рассеивающей среды, и долей диффузного света, отраженного на границе раздела сред: может быть легко найдена как решение уравнения (3.9а). Для решения уравнения (3.9б) его необходимо дополнить граничным условием. Граничное условие переизлучения [21] устанавливает соотношение между диффузным светом, направленным вглубь рассеивающей среды, и долей диффузного света, отраженного на границе раздела сред:
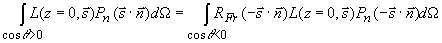 (3.10) (3.10)
где  - френелевский коэффициент отражения для неполяризованного света (см. - френелевский коэффициент отражения для неполяризованного света (см. [21]).
Общий подход к решению уравнения (3.9б) заключается в том, что диффузная составляющая лучевой интенсивности представляется в виде разложения по полиномам Лежандра [40,42]:
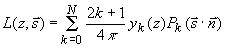 (3.11а) (3.11а)
где 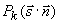 - полином Лежандра k-го порядка ( - полином Лежандра k-го порядка (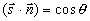 , где , где 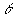 - угол между осью 0z и направлением движения фотона внутри среды). Для того, чтобы воспользоваться предложенным методом решения (3.9б) необходимо также записать разложение для фазовой функции - угол между осью 0z и направлением движения фотона внутри среды). Для того, чтобы воспользоваться предложенным методом решения (3.9б) необходимо также записать разложение для фазовой функции 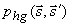 и функции источника рассеяного поля и функции источника рассеяного поля  : :
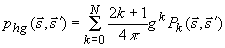 (3.11б) (3.11б)
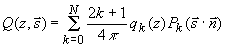 (3.11в) (3.11в)
Как показано в [44], коффициенты разложения функции источника 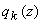 могут быть представлены в виде: могут быть представлены в виде:
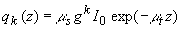 (3.12) (3.12)
Подставляя (3.11а),(3.11б) и (3.11в) в уравнение (3.9б), умножая последовательно на 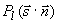 , где l , где l = (0, 1, …, N) , и интегрируя по полному телесному углу  , с учетом ортогональности соответствующих полиномов Лежандра, получим систему (N+1) независимых дифференциальных уравнений для коэффициентов разложения , с учетом ортогональности соответствующих полиномов Лежандра, получим систему (N+1) независимых дифференциальных уравнений для коэффициентов разложения 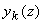 диффузной компоненты лучевой интенсивности. Затем, подставив полученные значения диффузной компоненты лучевой интенсивности. Затем, подставив полученные значения 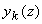 в (3.11а), можно просуммировать получившийся ряд и найти величину в (3.11а), можно просуммировать получившийся ряд и найти величину 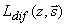 , и, следовательно, используя (3.8), - диффузную компоненту интенсивности света , и, следовательно, используя (3.8), - диффузную компоненту интенсивности света 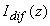 в исследуемой среде. в исследуемой среде.
Так как решить систему из бесконечного числа дифференциальных уравнений в принципе невозможно, число членов ряда в (3.11а) ограничивают. Рассмотренное в начале раздела диффузионное приближение получается, если положить в (3.11а) N=1, т. е. представить диффузную компоненту лучевой интенсивности в виде разложения по полиномам Лежандра 0-го и 1-го порядков:
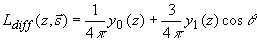 (3.13) (3.13)
где 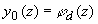 - интенсивность света в исследуемой рассеивающей среде, - интенсивность света в исследуемой рассеивающей среде, 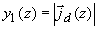 - модуль потока фотонов в среде. Тогда: - модуль потока фотонов в среде. Тогда:
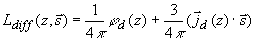 (3.14) (3.14)
Очевидно, что представить ряд (3.11а) в виде (3.14) с достаточной точностью можно только в том случае, когда, во-первых, коэффициенты 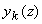 в (3.11а) убывают достаточно быстро с ростом k, а, во-вторых, второе слагаемое в (3.14) заметно меньше первого. Последнее требование можно считать выполненным, если фотон уже испытал на своем пути в исследуемой среде 2-3 акта рассеяния в (3.11а) убывают достаточно быстро с ростом k, а, во-вторых, второе слагаемое в (3.14) заметно меньше первого. Последнее требование можно считать выполненным, если фотон уже испытал на своем пути в исследуемой среде 2-3 акта рассеяния [40,44] , т. е. на глубине 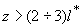 . Поэтому, как и указывалось выше, диффузионная теория достаточно точно описывает пространственное распределение интенсивности света H . Поэтому, как и указывалось выше, диффузионная теория достаточно точно описывает пространственное распределение интенсивности света H( z) в исследуемой рассеивающей среде только на растояниях 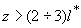 . Для расчета величины H . Для расчета величины H( z) на меньших глубинах необходимо использовать в (3.11а) более высокие порядки разложения, причем точность расчетов будет тем выше, чем больше N.
Полагая в (3.11а) N=5 получим следующую систему дифференциальных уравнений для коэффициентов разложения 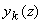 диффузной компоненты лучевой интенсивности по полиномам Лежандра [ диффузной компоненты лучевой интенсивности по полиномам Лежандра [42]:
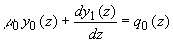 (3.15а) (3.15а)
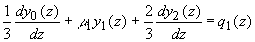 (3.15б) (3.15б)
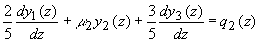 (3.15в) (3.15в)
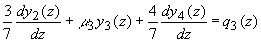 (3.15г) (3.15г)
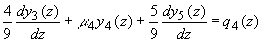 (3.15д) (3.15д)
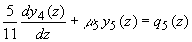 (3.15е) (3.15е)
где 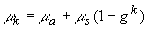 , а , а  определяются формулой (3.12). Граничное условие (3.10) подстановкой (3.11а) сводится к следующему виду: определяются формулой (3.12). Граничное условие (3.10) подстановкой (3.11а) сводится к следующему виду:
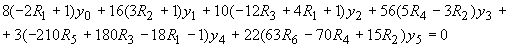 (3.16а) (3.16а)
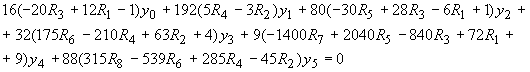 (3.16б) (3.16б)
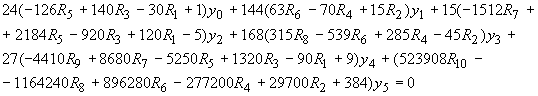 (3.16в) (3.16в)
где все 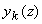 берутся при z=0, а берутся при z=0, а
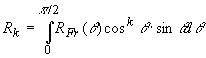 (3.17) (3.17)
Решение системы (3.15) можно получить в виде:
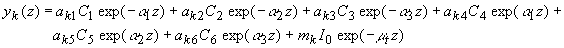 (3.18) (3.18)
где 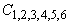 - произвольные константы, а - произвольные константы, а 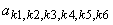 , 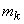 и и 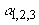 являются сложными функциями оптических характеристик исследуемой среды - коэффициента поглощения света являются сложными функциями оптических характеристик исследуемой среды - коэффициента поглощения света 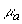 , коэффициента рассеяния света , коэффициента рассеяния света 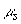 и показателя анизотропии g - и рассчитываются при решении системы (3.15) с использованием ЭВМ. Из условия и показателя анизотропии g - и рассчитываются при решении системы (3.15) с использованием ЭВМ. Из условия 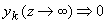 (на бесконечности диифузная интенсивность в среде должна обращаться в 0) следует, что (на бесконечности диифузная интенсивность в среде должна обращаться в 0) следует, что 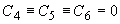 . Остальные три произвольные константы как функции известных величин . Остальные три произвольные константы как функции известных величин  и и  могут быть легко получены с помощью системы (3.16). могут быть легко получены с помощью системы (3.16).
Интенсивность диффузной составляющей света 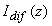 можно определить, подставляя величину можно определить, подставляя величину 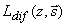 в виде ряда (3.11а) с коэффициентами разложения в виде ряда (3.11а) с коэффициентами разложения 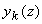 , определяемыми (3.18) в формулу (3.8): , определяемыми (3.18) в формулу (3.8):
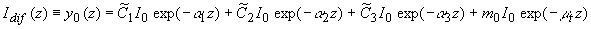 (3.19) (3.19)
где учтено, что 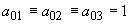 , 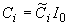 . Нормировав (3.19) на величину интенсивности падающего лазерного излучения . Нормировав (3.19) на величину интенсивности падающего лазерного излучения 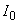 , окончательно получаем выражение для пространственного распределения интенсивности света H , окончательно получаем выражение для пространственного распределения интенсивности света H( z) в исследуемой рассеивающей среде в P 5-приближении:
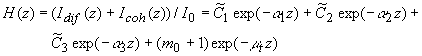 (3.20) (3.20)
где 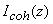 определяется формулой (3. определяется формулой (3.1).
Таким образом, рассмотренное P 5-приближение позволяет производить расчет величины H( z) в исследуемой среде с известными оптическими характеристиками - коэффициентом поглощения света  , коэффициентом рассеяния света , коэффициентом рассеяния света  и показателем анизотропии g. Как известно и показателем анизотропии g. Как известно [32,34] , характерной особенностью любой рассеивающей свет среды является наличие локального максимума интенсивности света в приповерхностном слое среды. Полагая
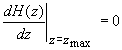 (3.21) (3.21)
можно, используя (3.20), найти положение 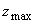 максимума интенсивности света в исследуемой среде. Следует отметить, что получение аналитического выражения для максимума интенсивности света в исследуемой среде. Следует отметить, что получение аналитического выражения для 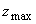 как функции оптических характеристик среды затруднительно с точки зрения математики (в формуле (3.21) стоит сумма четырех экспонент). Кроме того, величины как функции оптических характеристик среды затруднительно с точки зрения математики (в формуле (3.21) стоит сумма четырех экспонент). Кроме того, величины  , 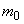 и и 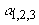 сами являются весьма сложными функциями оптических характеристик среды, и аналитические выражения для этих величин не могут быть аккуратно упрощены даже в приближении сами являются весьма сложными функциями оптических характеристик среды, и аналитические выражения для этих величин не могут быть аккуратно упрощены даже в приближении 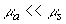 и и 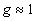 . Тем не менее для известных значений . Тем не менее для известных значений 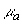 , 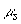 , и g положение максимума интенсивности света , и g положение максимума интенсивности света 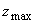 в исследуемой среде может быть определено по профилю H в исследуемой среде может быть определено по профилю H( z), рассчитанному с использованием формулы (3.20).
Исследование особенностей пространственного распределения интенсивности света H( z) в сильнорассеивающих средах можно проводить при помощи численного моделирования методом Монте-Карло (см. разд.1). Результаты моделирования [34,38] показывают, что в случае 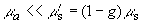 положение максимума интенсивности света положение максимума интенсивности света 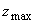 в сильнорассеивающей среде определяется только транспортной длиной свободного пробега фотона и эффективным коэффициентом отражения диффузного излучения от границы раздела и не зависит от величины коэффициента поглощения света в сильнорассеивающей среде определяется только транспортной длиной свободного пробега фотона и эффективным коэффициентом отражения диффузного излучения от границы раздела и не зависит от величины коэффициента поглощения света 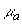 . Если величина фактора анизотропии рассеяния света . Если величина фактора анизотропии рассеяния света  0.78, положение максимума интенсивности света 0.78, положение максимума интенсивности света 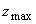 в исследуемой среде описывается формулой в исследуемой среде описывается формулой [34]:
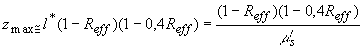 (3.22) (3.22)
В то же время было показано, что H( z) при 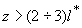 совпадает с распределением h совпадает с распределением h( z) (3.7). Поэтому на таких расстояниях диффузионное приближение, рассмотренное в начале этого раздела, применимо для расчета пространственного распределения интенсивности света в рассеивающей среде.
|
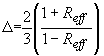 - постоянная, зависящая от соотношения показателей преломления прозрачной и рассеивающей сред,
- постоянная, зависящая от соотношения показателей преломления прозрачной и рассеивающей сред, 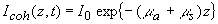 (3.1)
(3.1)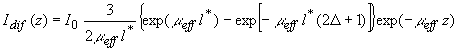 (3.2)
(3.2)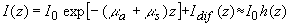 (3.3)
(3.3)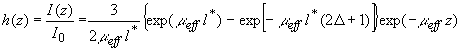 (3.4)
(3.4)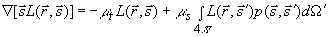 (3.5)
(3.5)
 (3.6)
(3.6)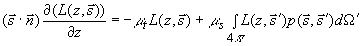 (3.7)
(3.7)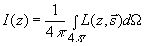 (3.8)
(3.8)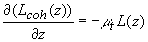 (3.9а)
(3.9а)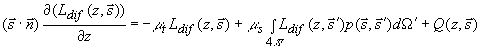 (3.9б)
(3.9б)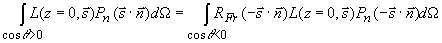 (3.10)
(3.10)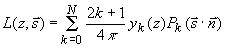 (3.11а)
(3.11а)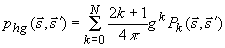 (3.11б)
(3.11б)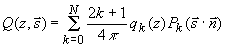 (3.11в)
(3.11в)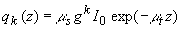 (3.12)
(3.12)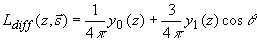 (3.13)
(3.13)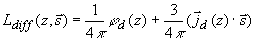 (3.14)
(3.14)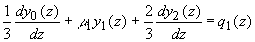 (3.15б)
(3.15б)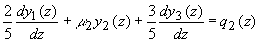 (3.15в)
(3.15в)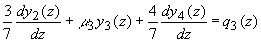 (3.15г)
(3.15г)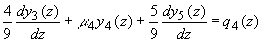 (3.15д)
(3.15д)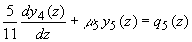 (3.15е)
(3.15е)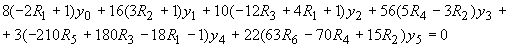 (3.16а)
(3.16а)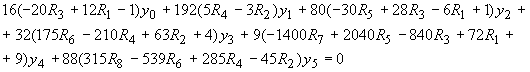 (3.16б)
(3.16б)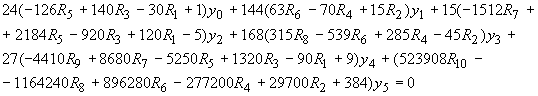 (3.16в)
(3.16в)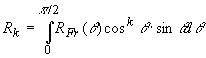 (3.17)
(3.17)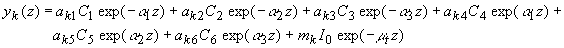 (3.18)
(3.18)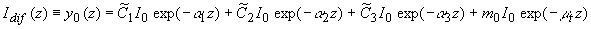 (3.19)
(3.19)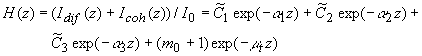 (3.20)
(3.20)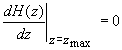 (3.21)
(3.21)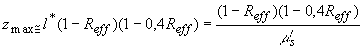 (3.22)
(3.22)