1.2. Временные профили оптико-акустических сигналов и их трансформация при распространении в линейной среде.
Метод передаточных функций, использованный в предыдущем параграфе, позволяет найти спектр ОА сигнала. Как не трудно заметить, однако, такой подход может быть применен только в том случае, когда нелинейные, дифракционные и диссипативные явления проявляются слабо в зоне генерации, т.е.
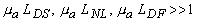 (1.2.1)
(1.2.1)
где
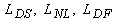 - соответственно характерные длины затухания, нелинейности и дифракции звука. Указанные соотношения (1.2.1) позволяют анализировать тепловое возбуждение звука поэтапно. На первом этапе рассматривается задача о тепловом возбуждении звука в отсутствии диссипативных, дифракционных и нелинейных эффектов. На втором - эволюция профиля ОА импульса в нелинейной диссипативной среде при ограниченных поперечных размерах пучка [4] и в отсутствии тепловых источников.
- соответственно характерные длины затухания, нелинейности и дифракции звука. Указанные соотношения (1.2.1) позволяют анализировать тепловое возбуждение звука поэтапно. На первом этапе рассматривается задача о тепловом возбуждении звука в отсутствии диссипативных, дифракционных и нелинейных эффектов. На втором - эволюция профиля ОА импульса в нелинейной диссипативной среде при ограниченных поперечных размерах пучка [4] и в отсутствии тепловых источников.
Уравнение, описывающее такую эволюцию волны, - уравнение Хохлова-Заболотской-Кузнецова [5] - может быть записано в виде:
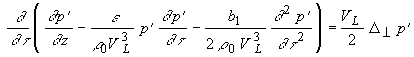 (1.2.2)
(1.2.2)
где e
- нелинейный акустический параметр поглощающей среды,
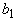 - коэффициент диссипации. В случае, когда ОА сигнал распространяется и регистрируется в прозрачной среде (косвенная схема регистрации), в (1.2.2) нужно заменить
- коэффициент диссипации. В случае, когда ОА сигнал распространяется и регистрируется в прозрачной среде (косвенная схема регистрации), в (1.2.2) нужно заменить 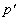 на
на 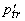
,
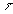 - на
- на 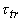 и все параметры поглощающей среды - на соответствующие им значения для прозрачной среды.
и все параметры поглощающей среды - на соответствующие им значения для прозрачной среды.
В общем случае решение (1.2.2) возможно только численным образом. Аналитические результаты могут быть получены в случаях сильного различия масштабов проявления отдельных эффектов. При распространении ультразвука в твердых телах влияние нелинейных искажений на профиль ОА сигнала (даже при его амплитуде в десятки атмосфер) существенно слабее, чем влияние диссипации и дифракции [3]. Поэтому ограничимся рассмотрением двух последних факторов.
Если
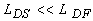 , то уравнение (1.2.2) значительно упрощается и имеет следующий вид:
, то уравнение (1.2.2) значительно упрощается и имеет следующий вид:
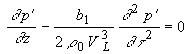 (1.2.3)
(1.2.3)
частотный спектр решения которого представим в виде
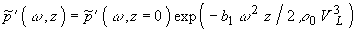 (1.2.4)
(1.2.4)
В качестве граничного условия
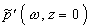 используется решение задачи термооптического возбуждения звука (1.1.2). Соответственно временное представление будет иметь вид:
используется решение задачи термооптического возбуждения звука (1.1.2). Соответственно временное представление будет иметь вид:
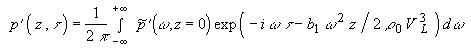 (1.2.5)
(1.2.5)
Решение (1.2.4) показывает, что в этом случае спектр возбуждаемой волны домножается на диссипативный фактор, который приводит к прогрессирующему по мере распространения затуханию высокочастотных компонент сигнала. Поэтому под влиянием диссипации происходит сглаживание резких градиентов во временном профиле сигнала.
На больших расстояниях
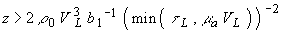 спектр ОА сигнала ограничивается диссипативным фактором и профиль сигнала имеет универсальный гауссовый вид:
спектр ОА сигнала ограничивается диссипативным фактором и профиль сигнала имеет универсальный гауссовый вид:
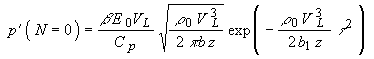 (1.2.6)
(1.2.6)
- для жесткой границы поглощающей среды и его производной
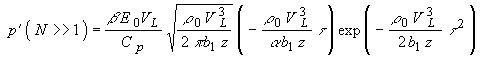 (1.2.7)
(1.2.7)
- для свободной границы (
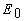 - плотность энергии, падающего на среду излучения). Амплитуда возбуждаемого при жесткой границе ОА сигнала убывает в диссипативной среде пропорционально
- плотность энергии, падающего на среду излучения). Амплитуда возбуждаемого при жесткой границе ОА сигнала убывает в диссипативной среде пропорционально 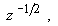 при свободной - пропорционально
при свободной - пропорционально 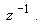 На расстояниях
На расстояниях 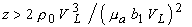 профиль сигнала имеет универсальную форму и все детали распределения тепловых источников звука стираются.
профиль сигнала имеет универсальную форму и все детали распределения тепловых источников звука стираются.
При термооптическом возбуждении звука радиус акустического пучка на поверхности поглощающей среды
z=0 совпадает с радиусом лазерного пучка 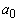 . В зависимости от соотношения радиуса пучка
. В зависимости от соотношения радиуса пучка 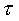 и глубины проникновения света
и глубины проникновения света 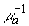 фазовый фронт акустической волны может быть близким к плоскому (
фазовый фронт акустической волны может быть близким к плоскому (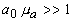 ), цилиндрическому (
), цилиндрическому (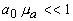 ) или сферическому (
) или сферическому (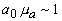
).
В случае цилиндрического и сферического фазового фронта профиль оптико-акустического сигнала не изменяется при распространении [6]. Если же исходно фронт волны близок к плоскому, то ситуация несколько сложнее. На расстояниях
z порядка 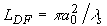
(
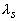 - длина звуковой волны) пучок расплывается (поперечное сечение увеличивается в два раза) за счет дифракции [7]; на расстояниях
- длина звуковой волны) пучок расплывается (поперечное сечение увеличивается в два раза) за счет дифракции [7]; на расстояниях 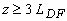 фронт волны становится близок к сферическому. Отличительной особенностью оптико-акустических сигналов является широкий диапазон содержащихся в них частот. Поэтому длины волн гармонических составляющих сигнала изменяются в широких пределах и, соответственно, длины дифракции
фронт волны становится близок к сферическому. Отличительной особенностью оптико-акустических сигналов является широкий диапазон содержащихся в них частот. Поэтому длины волн гармонических составляющих сигнала изменяются в широких пределах и, соответственно, длины дифракции 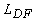 отдельных гармоник существенно различны. Низкочастотные составляющие спектра дифрагируют быстрее высокочастотных (на меньших расстояниях). В то же время, для достижения высокого пространственного разрешения необходимо зарегистрировать сигнал в возможно более широкой полосе частот. Поэтому наиболее целесообразно регистрировать акустическую волну, распространяющуюся по нормали к границе поглощающей среды.
отдельных гармоник существенно различны. Низкочастотные составляющие спектра дифрагируют быстрее высокочастотных (на меньших расстояниях). В то же время, для достижения высокого пространственного разрешения необходимо зарегистрировать сигнал в возможно более широкой полосе частот. Поэтому наиболее целесообразно регистрировать акустическую волну, распространяющуюся по нормали к границе поглощающей среды.
Если для всех гармоник ОА сигнала выполнено соотношение
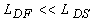 , то уравнение (1.2.2) сводится к параболическому уравнению теории дифракции [3, 8]:
, то уравнение (1.2.2) сводится к параболическому уравнению теории дифракции [3, 8]:
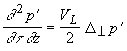 (1.2.8)
(1.2.8)
Считая поперечное распределение интенсивности света в пучке гауссовым, граничное условие задачи дифракции можно записать в виде:
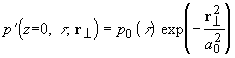 (1.2.9)
(1.2.9)
где
 - профиль волны на границе поглощающей среды. При распространении импульса для каждой из гармонических составляющих в (1.2.9) гауссово поперечное распределение сохраняется и решение может быть записано в виде:
- профиль волны на границе поглощающей среды. При распространении импульса для каждой из гармонических составляющих в (1.2.9) гауссово поперечное распределение сохраняется и решение может быть записано в виде:
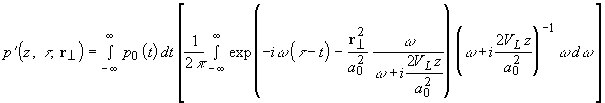 (1.2.10)
(1.2.10)
На оси пучка (
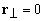 ) решение (1.2.10) может быть упрощено [9]:
) решение (1.2.10) может быть упрощено [9]:
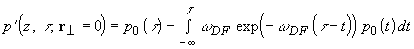 (1.2.11)
(1.2.11)
где
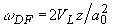 . Первое слагаемое в (1.2.11) повторяет форму сигнала на границе и соответствует решению в случае плоской волны; второе слагаемое описывает влияние ограниченности ширины пучка. Характерная частота
. Первое слагаемое в (1.2.11) повторяет форму сигнала на границе и соответствует решению в случае плоской волны; второе слагаемое описывает влияние ограниченности ширины пучка. Характерная частота 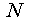 (“дифракционная” частота) растет с увеличением расстояния z и с уменьшением площади поперечного сечения пучка. В дальней волновой зоне (
(“дифракционная” частота) растет с увеличением расстояния z и с уменьшением площади поперечного сечения пучка. В дальней волновой зоне (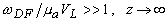 ) решение (1.2.11) переходит в
) решение (1.2.11) переходит в
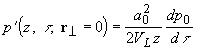 (1.2.12)
(1.2.12)
Как видно из (1.2.12), в дальней зоне профиль волны переходит в производную профиля на границе и его амплитуда убывает обратно пропорционально пройденному волной расстоянию.
Для случая однородного поглощения света (
 ) и короткого лазерного импульса (
) и короткого лазерного импульса (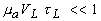 , интеграл (1.2.11) удается выразить в элементарных функциях [9]:
, интеграл (1.2.11) удается выразить в элементарных функциях [9]:
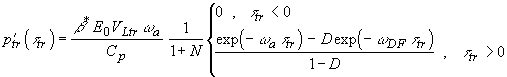 (1.2.13)
(1.2.13)
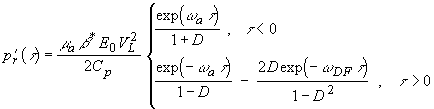 (1.2.14)
(1.2.14)
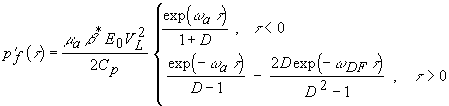 (1.2.15)
(1.2.15)
где
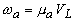 - характерная частота спектра оптико-акустического сигнала,
- характерная частота спектра оптико-акустического сигнала, 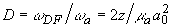 - безразмерное расстояние, выраженное в длинах дифракции
- безразмерное расстояние, выраженное в длинах дифракции 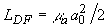 на частоте
на частоте 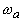 . Формула (1.2.14) получена для акустически жесткой границы поглощающей среды; формула (1.2.15) - для свободной границы. В общем случае конечного
. Формула (1.2.14) получена для акустически жесткой границы поглощающей среды; формула (1.2.15) - для свободной границы. В общем случае конечного 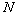 решение может быть выражено через представленные решения
решение может быть выражено через представленные решения 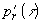 и
и 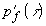
:
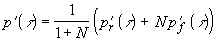 (1.2.16)
(1.2.16)
Как видно из формул (1.2.14) и (1.2.15), передний фронт сигнала (
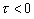 ) при прямой регистрации сохраняет экспоненциальную форму на любом расстоянии от границы. При
) при прямой регистрации сохраняет экспоненциальную форму на любом расстоянии от границы. При 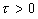 сигнал образуется разностью двух экспонент с показателями, определяемыми коэффициентом поглощения света (
сигнал образуется разностью двух экспонент с показателями, определяемыми коэффициентом поглощения света (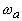 ) и дифракцией (
) и дифракцией (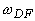 ). В зависимости от их соотношения (величины D) каждая из них проявляется либо при малых, либо при больших
). В зависимости от их соотношения (величины D) каждая из них проявляется либо при малых, либо при больших 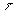 . На малых расстояниях (
. На малых расстояниях (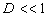 ) при малых
) при малых 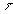 профиль ОА-сигнала определяется поглощением света, а дифракционное слагаемое будет существенно только при
профиль ОА-сигнала определяется поглощением света, а дифракционное слагаемое будет существенно только при 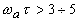 . На больших расстояниях (
. На больших расстояниях (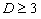 ) - наоборот, при малых
) - наоборот, при малых 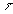
(
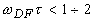 ) сигнал изменяется по экспоненте с показателем
) сигнал изменяется по экспоненте с показателем 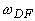 , а при
, а при 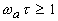 - с показателем
- с показателем 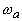
.
Дифракционная трансформация оптико-акустических сигналов для различных значений
D при прямой и косвенной регистрации приведена на рис.1.2.1.
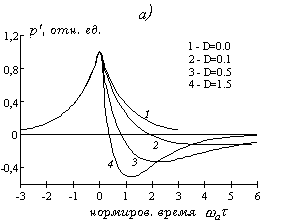
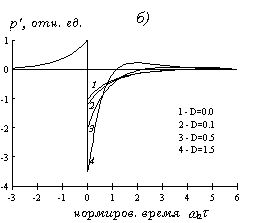
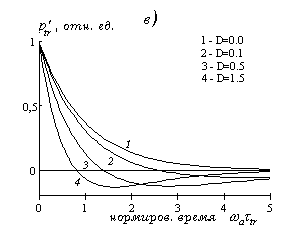
Рис.1.2.1.
Дифракционная трансформация ОА сигнала при прямой и косвенной регистрации: (а) - жесткая граница поглощающей среды, (б) - свободная граница поглощающей среды, (в) - косвенная регистрация.
При прямой регистрации и жесткой границе (рис.1.2.1а) первоначально симметричный импульс сжатия по мере распространения (увеличения значения
D) приобретает вид следующих друг за другом импульсов сжатия и разрежения. Как видно, даже на достаточно малых расстояниях ( ) фаза разрежения проявляется весьма заметно. При свободной границе (рис.1.2.1б) первоначальный импульс, содержавший фазу сжатия и фазу разрежения, приобретает сложный "трехполярный" характер: амплитуда фазы разрежения относительно возрастает, и ее длительность укорачивается; следом за ней появляется вторая фаза сжатия. И при жесткой, и при свободной границе временная форма переднего фронта (
) фаза разрежения проявляется весьма заметно. При свободной границе (рис.1.2.1б) первоначальный импульс, содержавший фазу сжатия и фазу разрежения, приобретает сложный "трехполярный" характер: амплитуда фазы разрежения относительно возрастает, и ее длительность укорачивается; следом за ней появляется вторая фаза сжатия. И при жесткой, и при свободной границе временная форма переднего фронта ( ) не искажается при дифракции.
) не искажается при дифракции.
При косвенной регистрации сигнала (рис.1.2.1в) распространяющийся в прозрачной среде ОА сигнал имеет резкий передний фронт (с временем нарастания порядка длительности лазерного импульса) и затем спад, определяемый разностью двух экспонент. Первоначальный импульс сжатия укорачивается и появляется следующий за ним импульс разрежения.
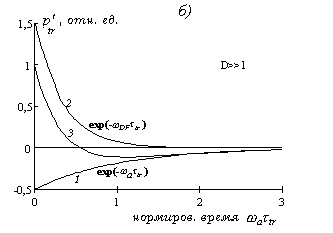
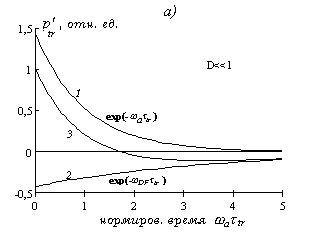
Рис.1.2.2. Составляющие ОА сигнала при косвенной регистрации: (а) - на малых расстояниях, (б) - в дальней волновой зоне. 1 - экспонента, обусловленная поглощением света, 2 - экспонента, обусловленная дифракцией, 3 - результирующий сигнал.
На малых расстояниях или при достаточно большом поглощении света (
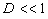 , рис.1.
, рис.1.2.2
а) спад сигнала (
3) сначала следует экспоненте с показателем 
(
1) (при  ), а в дальнейшем - экспоненте с показателем
), а в дальнейшем - экспоненте с показателем 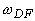
(
2) (
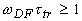 ) (см. рис.1.2.2а). При переходе в дальнюю зону или при слабом поглощении света (
) (см. рис.1.2.2а). При переходе в дальнюю зону или при слабом поглощении света (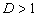 ) картина меняется на обратную. При
) картина меняется на обратную. При 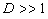 (рис.1.2.2б) ОА сигнал будет состоять из короткого импульса с длительностью
(рис.1.2.2б) ОА сигнал будет состоять из короткого импульса с длительностью 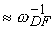 на экспоненциальном пьедестале с показателем убывания
на экспоненциальном пьедестале с показателем убывания 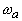
.
Если ОА сигнал зарегистрирован на известном расстоянии
z=L (в поглощающей или прозрачной среде), то по его временному профилю 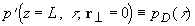 с учетом дифракционных искажений можно восстановить
с учетом дифракционных искажений можно восстановить 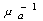 (см. (1.2.11)).
(см. (1.2.11)).
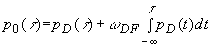 (1.2.17)
(1.2.17)
где в данном случае
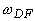 - частота волны, для которой длина дифракции
- частота волны, для которой длина дифракции 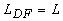
.
Соотношение масштабов проявления дифракционных и диссипативных явлений описывается безразмерным числом
 (1.2.18)
(1.2.18)
которое пропорционально кубу частоты. На высоких частотах преобладает диссипация, на низких - дифракция.
Таким образом, поэтапный подход позволяет рассчитать форму ОА сигнала, возбуждаемого в поглощающей среде с известными теплофизическими параметрами, и проанализировать диссипативные и дифракционные искажения импульса при распространении в исследуемой среде. Использование данного метода, как будет показано ниже, дает возможность провести широкие исследования оптических, акустических и механических свойств гетерогенных сред.
 - профиль волны на границе поглощающей среды. При распространении импульса для каждой из гармонических составляющих в (1.2.9) гауссово поперечное распределение сохраняется и решение может быть записано в виде:
- профиль волны на границе поглощающей среды. При распространении импульса для каждой из гармонических составляющих в (1.2.9) гауссово поперечное распределение сохраняется и решение может быть записано в виде:




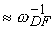 на экспоненциальном пьедестале с показателем убывания
на экспоненциальном пьедестале с показателем убывания 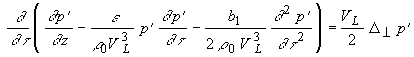 (1.2.2)
(1.2.2)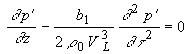 (1.2.3)
(1.2.3)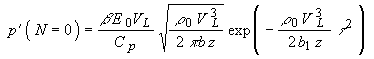 (1.2.6)
(1.2.6)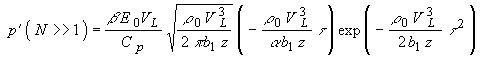 (1.2.7)
(1.2.7)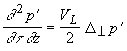 (1.2.8)
(1.2.8)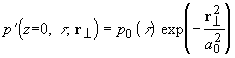 (1.2.9)
(1.2.9)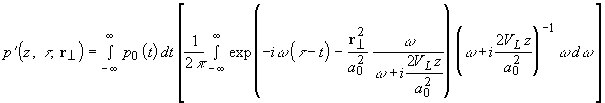 (1.2.10)
(1.2.10)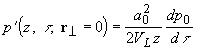 (1.2.12)
(1.2.12)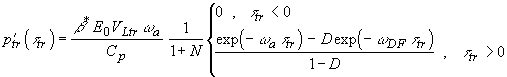 (1.2.13)
(1.2.13)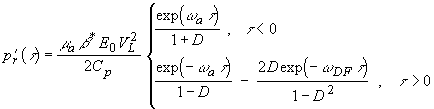 (1.2.14)
(1.2.14)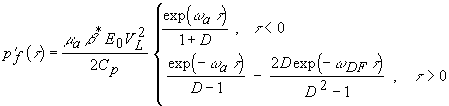 (1.2.15)
(1.2.15)
 (1.2.18)
(1.2.18)