§
2.2. Теоретический расчет пространственного распределения интенсивности света в условиях многократного рассеяния.
Рассмотрим полубесконечную среду с коэффициентами поглощения и рассеяния света ma и ms соответственно и, занимающую полупространство z>0. Пусть рассеяние является изотропным и преобладает над поглощением (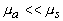 ), то есть в среде реализуется режим многократного рассеяния излучения [32]. При падении на такую среду светового импульса с плоским волновым фронтом (временная зависимость интенсивности ), то есть в среде реализуется режим многократного рассеяния излучения [32]. При падении на такую среду светового импульса с плоским волновым фронтом (временная зависимость интенсивности 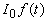 , характерная длительность импульса , характерная длительность импульса 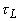 ) интенсивность излучения внутри среды может быть представлена как сумма ослабленного первичного пучка фотонов, еще не претерпевших рассеяние, ) интенсивность излучения внутри среды может быть представлена как сумма ослабленного первичного пучка фотонов, еще не претерпевших рассеяние, 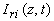 и диффузного поля рассеянного света и диффузного поля рассеянного света 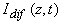 . Первая из этих составляющих быстро спадает с увеличением z [32]: . Первая из этих составляющих быстро спадает с увеличением z [32]:
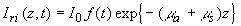 (2.2.1) (2.2.1)
Для нахождения диффузной компоненты интенсивности воспользуемся уравнением баланса фотонов:
q0 - qs - qa = 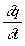 (2.2.2) (2.2.2)
где q0, qs, qa, соответственно число фотонов в единицу объема в единичном телесном угле  рождающихся в среде, рассеянных и поглощенных за единицу времени. Тогда величина рождающихся в среде, рассеянных и поглощенных за единицу времени. Тогда величина
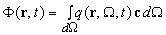 (2.2.3) (2.2.3)
является полным скалярным потоком фотонов через единичную площадку в единицу времени, а 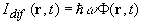 - полной интенсивностью диффузного света в рассеивающей среде. - полной интенсивностью диффузного света в рассеивающей среде.
Рассмотрим маленькую площадку 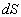 , лежащую внутри рассеивающей среды в плоскости (x , лежащую внутри рассеивающей среды в плоскости (x, y) в координатной системе, представленной на рис.2.2.1.
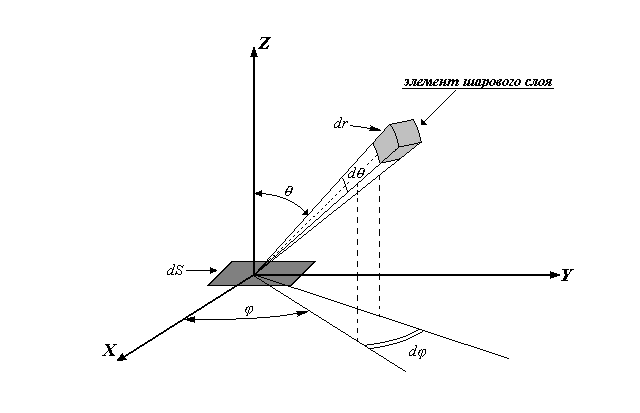
Рис.2.2.1 Система координат для расчета диффузного поля.
Число фотонов, рассеянных в единичном объеме 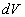 , расположенном в точке с координатами , расположенном в точке с координатами 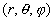 , за единицу времени составит , за единицу времени составит 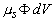 . Предположим вначале, что рассеяние является изотропным. Тогда вероятность того, что фотон рассеется в направлении площадки . Предположим вначале, что рассеяние является изотропным. Тогда вероятность того, что фотон рассеется в направлении площадки 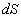 , т.е. в направлении, определяемым телесным углом , т.е. в направлении, определяемым телесным углом 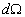 , составит , составит 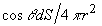 . Предположим также, что в среде отсутствует поглощение. Вероятность того, что фотон, рассеянный единичным объемом . Предположим также, что в среде отсутствует поглощение. Вероятность того, что фотон, рассеянный единичным объемом 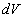 в направлении в направлении 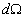 достигнет рассматриваемую площадку равна достигнет рассматриваемую площадку равна 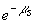 . Следовательно, число фотонов, рассеянных единичным объемом . Следовательно, число фотонов, рассеянных единичным объемом 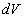 в направлении в направлении 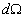 , составит: , составит:
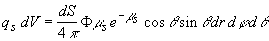 (2.2.4) (2.2.4)
Если 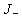 - плотность тока фотонов в отрицательное z направление, то полное число фотонов, проходящих за единицу времени через площадку - плотность тока фотонов в отрицательное z направление, то полное число фотонов, проходящих за единицу времени через площадку 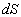 в отрицательное z направление составит в отрицательное z направление составит
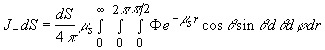 (2.2.5) (2.2.5)
Для вычисления интеграла необходимо знать 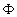 как функцию пространственных координат, поэтому разложим как функцию пространственных координат, поэтому разложим 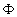 в ряд Тейлора на поверхности в ряд Тейлора на поверхности 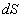 [33]:
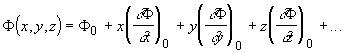 (2.2.6) (2.2.6)
Вводя сферические координаты и проводя интегрирование, получим:
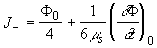 (2.2.7а) (2.2.7а)
Аналогично, плотность тока фотонов в положительном z направлении
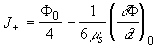 (2.2.7б) (2.2.7б)
Следовательно, полная плотность тока в z направлении
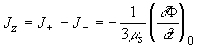 (2.2.7в) (2.2.7в)
В (2.2.6) были учтены только первые члены разложения, потому что члены второго порядка дают одинаковые вклады в 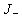 и и 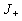 ; так, полная плотность тока через поверхность ; так, полная плотность тока через поверхность 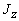 не меняется. Если единичная площадка не меняется. Если единичная площадка 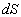 расположена произвольно в координатной системе, то расположена произвольно в координатной системе, то
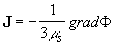 (2.2.8) (2.2.8)
Величина 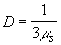 называется коэффициентом диффузии для потока фотонов называется коэффициентом диффузии для потока фотонов [33, 34] . Если в рассеивающей среде существует поглощение, причем 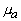 << 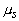 + 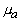 , и рассеяние не является изотропным, то выражение для D должно быть скорректировано с учетом индикатрисы рассеяния и поглощения незначительной части излучения , и рассеяние не является изотропным, то выражение для D должно быть скорректировано с учетом индикатрисы рассеяния и поглощения незначительной части излучения [34]:
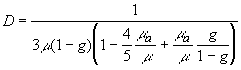 (2.2.9) (2.2.9)
где 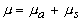 - коэффициент полного ослабления. - коэффициент полного ослабления.
Обычно при рассмотрении диффузии фотонов в сильнорассеивающих средах используют выражение:
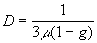 (2.2.10) (2.2.10)
а величину 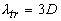 называют средней транспортной длиной свободного пробега фотона. называют средней транспортной длиной свободного пробега фотона.
Следовательно, число фотонов, рассеянных в единичном объеме за единицу времени составит
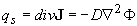 (2.2.11) (2.2.11)
Учитывая, что число фотонов, поглощенных в единичном объеме за единицу времени
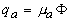 (2.2.12) (2.2.12)
получим искомое уравнение диффузии в следующем виде:
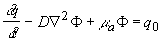 (2.2.13) (2.2.13)
Домножая обе части уравнения на 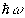 , перепишем (2.2.13) в виде: , перепишем (2.2.13) в виде:
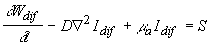 (2.2.14) (2.2.14)
где 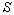 и и 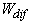 - соответственно распределение источников и объемная плотность энергии диффузионного поля в среде. Это уравнение достаточно хорошо описывает функцию - соответственно распределение источников и объемная плотность энергии диффузионного поля в среде. Это уравнение достаточно хорошо описывает функцию 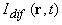 вдали от границы рассеивающей среды (при вдали от границы рассеивающей среды (при 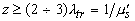 ) и источников излучения. ) и источников излучения.
Если время жизни фотона в среде  много меньше длительности лазерного импульса ( много меньше длительности лазерного импульса (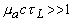 ), то можно считать процесс рассеяния света в среде квазистационарным. Учитывая также, что на рассеивающую среду падает плоская волна, окончательно получим одномерное стационарное уравнение диффузии ), то можно считать процесс рассеяния света в среде квазистационарным. Учитывая также, что на рассеивающую среду падает плоская волна, окончательно получим одномерное стационарное уравнение диффузии [15]:
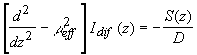 (2.2.15) (2.2.15)
где 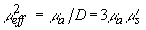 .
Для расчета пространственного распределения интенсивности света с среде необходимо дополнить это уравнение граничными условиями. Для простоты будем сначала считать, что показатели преломления прозрачной и рассеивающей сред одинаковы, т.е. отражение падающего на среду излучения отсутствует. Тогда, аналогично граничному условию для плотности тока в электродинамике (см., например, [32] ), положим равенство нормальных компонент плотности потока фотонов на границе раздела:
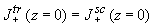 (2.2.16а) (2.2.16а)
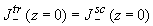 (2.2.16б) (2.2.16б)
где знаки (tr) и (sc) относятся, соответственно, к прозрачной и рассеивающей среде. Переписывая это условие для интенсивности, согласно (2.2.6) получим:
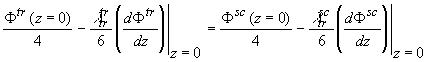 (2.2.17а) (2.2.17а)
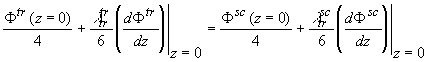 (2.2.17б) (2.2.17б)
Учитывая, что на границе (при 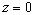 ) ) 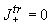 , т.е. в прозрачной среде отсутствует ток фотонов, направленный к границе рассеивающей среды, получим: , т.е. в прозрачной среде отсутствует ток фотонов, направленный к границе рассеивающей среды, получим:
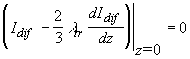 (2.2.18) (2.2.18)
Записанное граничное условие может быть приближенно заменено “линейно-экстраполированным” [37-39] (см. рис.2.2.2): функция 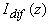 заменяется в прозрачной среде ее линейной экстраполяцией так, что наклон прямой соответствует заменяется в прозрачной среде ее линейной экстраполяцией так, что наклон прямой соответствует 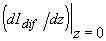 .
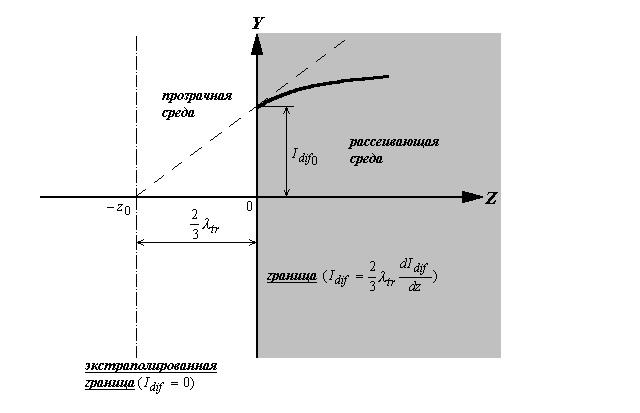
Рис.2.2.2 Экстраполяция граничного условия для уравнения диффузии фотонов.
Следовательно, расстояние 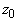 в прозрачной среде, на котором в прозрачной среде, на котором 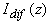 обращается в ноль, вычисляется из следующего соотношения: обращается в ноль, вычисляется из следующего соотношения:
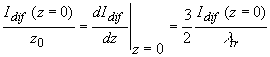 (2.2.19) (2.2.19)
т.е.
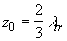 (2.2.20) (2.2.20)
Точное решение так называемой задачи Милна об отражении плоской световой волны от полубесконечной случайно-неоднородной среды [32] дает
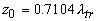 (2.2.21) (2.2.21)
В случае когда показатели преломления прозрачной (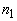 ) и рассеивающей ( ) и рассеивающей (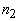 ) [39] не равны, при расчете необходимо принять во внимание отражение части излучения на границе рассеивающей среды. Это приводит к следующему результату [35, 36, 39]:
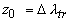 (2.2.22) (2.2.22)
где 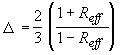 - постоянная, зависящая от соотношения показателей преломления прозрачной ( 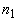 ) и рассеивающей ( 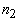 ) [39] сред; эффективный коэффициент отражения диффузного излучения от границы раздела:
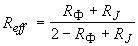 (2.2.23) (2.2.23)
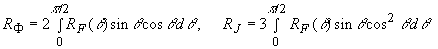 (2.2.24) (2.2.24)
где 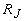 и и 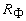 - соответственно коэффициенты отражения для скалярного потока и плотности тока фотонов. - соответственно коэффициенты отражения для скалярного потока и плотности тока фотонов.
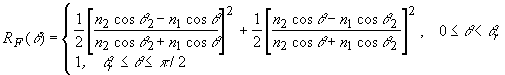 (2.2.25) (2.2.25)
где 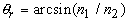 - угол полного внутреннего отражения, - угол полного внутреннего отражения, 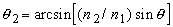 .
Таким образом, в первом приближении граничное условие для 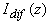 на поверхности среды и функцию распределения источников S на поверхности среды и функцию распределения источников S( z) можно представить в виде:
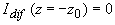 (2.2.26) (2.2.26)
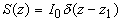 (2.2.27) (2.2.27)
где d( z)- дельта-функция Дирака, 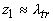 - глубина, на которой падающее на среду коллимированное излучение преобразуется в диффузное.
Решение уравнения (2.2.15) с граничным условием (2.2.26) и с учетом (2.2.27) при 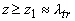 дает: дает:
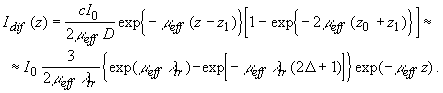 (2.2.28) (2.2.28)
Таким образом, интенсивность света внутри рассеивающей среды на расстояниях 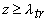
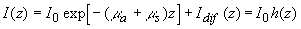 (2.2.29) (2.2.29)
где функция
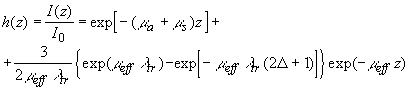 (2.2.30) (2.2.30)
описывает пространственное распределение интенсивности света в диффузионном приближении и на расстояниях 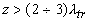 определяется только диффузной компонентой рассеянного светового поля (второе слагаемое в (2.2.30)), поскольку в приближении определяется только диффузной компонентой рассеянного светового поля (второе слагаемое в (2.2.30)), поскольку в приближении 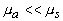 коэффициент экстинкции света коэффициент экстинкции света 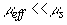 . Традиционно используемое выражение 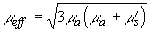 [19, 20] при 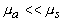 выходит за пределы точности модели и в рамках диффузионного приближения совпадает с введенным выше выражением (см. (2.2.10)). выходит за пределы точности модели и в рамках диффузионного приближения совпадает с введенным выше выражением (см. (2.2.10)).
В общем случае интенсивность света в рассеивающей среде представляется в виде 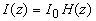 , однако в области , однако в области 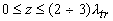 пространственное распределение интенсивности света в среде H пространственное распределение интенсивности света в среде H( z) не может быть выражено аналитической функцией [19, 20]. Численное моделирование методом Монте-Карло показывает, что H( z) имеет локальный минимум на границе рассеивающей среды z=0, а максимум интенсивности света наблюдается под поверхностью среды на глубине 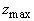 , определяемой транспортной длиной свободного пробега фотона и эффективным коэффициентом отражения диффузного излучения от границы рассеивающей и прозрачной сред и не зависящей от величины коэффициента поглощения света , определяемой транспортной длиной свободного пробега фотона и эффективным коэффициентом отражения диффузного излучения от границы рассеивающей и прозрачной сред и не зависящей от величины коэффициента поглощения света 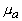 . Для . Для 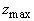 была найдена приближенная формула [27] была найдена приближенная формула [27]:
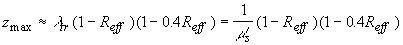 (2.2.31) (2.2.31)
В то же время, H( z) при 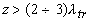 совпадает с распределением совпадает с распределением  (2.2.30). Поэтому на таких расстояниях диффузионное приближение применимо для расчета пространственного распределения интенсивности света в рассеивающей среде. (2.2.30). Поэтому на таких расстояниях диффузионное приближение применимо для расчета пространственного распределения интенсивности света в рассеивающей среде.
|
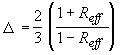 - постоянная, зависящая от соотношения показателей преломления прозрачной (
- постоянная, зависящая от соотношения показателей преломления прозрачной (
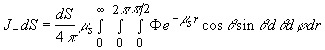 (2.2.5)
(2.2.5)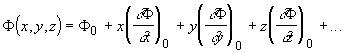 (2.2.6)
(2.2.6)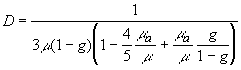 (2.2.9)
(2.2.9)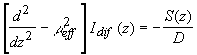 (2.2.15)
(2.2.15)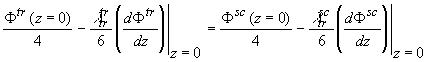 (2.2.17а)
(2.2.17а)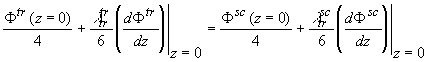 (2.2.17б)
(2.2.17б)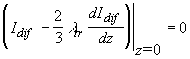 (2.2.18)
(2.2.18)
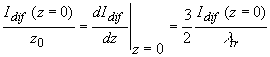 (2.2.19)
(2.2.19)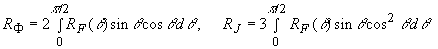 (2.2.24)
(2.2.24)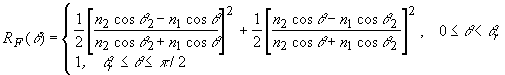 (2.2.25)
(2.2.25)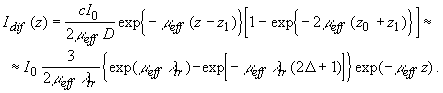 (2.2.28)
(2.2.28)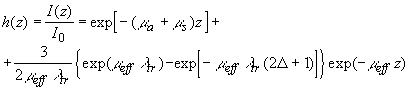 (2.2.30)
(2.2.30)