§
2.3. Теоретическая модель импульсного оптико-акустического эффекта в рассеивающей среде.
Решение задачи об импульсном лазерном возбуждении звука разбивается на три этапа: (1) - расчет плотности тепловыделения в рассеивающей среде; (2) - расчет теплового поля в среде, создаваемого найденными на первом этапе источниками тепла; (3) - нахождение акустического поля в среде, излучаемого рассчитанными выше тепловыми полями. Каждая из этих задач не имеет в общем случае аналитического решения. Поэтому анализ термооптического возбуждения звука в рассеивающей среде возможен только при дополнительных упрощающих предположениях.
Пусть среда является сильно рассеивающей (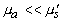 ) и ее толщина L и характерный радиус лазерного пучка
) и ее толщина L и характерный радиус лазерного пучка 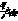 , используемого для возбуждения звука, много больше глубины проникновения света в среду
, используемого для возбуждения звука, много больше глубины проникновения света в среду 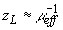 . Тогда можно использовать приближение полубесконечной среды и считать лазерный пучок коллимированным. Это позволяет воспользоваться результатами §
2.2 для решения оптической (первой) части задачи лазерного возбуждения звука и ограничиться одномерными акустической и тепловой задачами [3].
. Тогда можно использовать приближение полубесконечной среды и считать лазерный пучок коллимированным. Это позволяет воспользоваться результатами §
2.2 для решения оптической (первой) части задачи лазерного возбуждения звука и ограничиться одномерными акустической и тепловой задачами [3].
Будем считать, что исследуемая среда является акустически и термически однородной. Тогда ее можно описывать некоторыми "эффективными" параметрами - удельной теплоемкостью 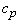 , скоростью звука
, скоростью звука 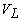 , коэффициентом теплового расширения b
, температуропроводностью
, коэффициентом теплового расширения b
, температуропроводностью 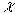 . Если время релаксации теплового поля в области нагрева
. Если время релаксации теплового поля в области нагрева 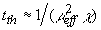 много больше длительности лазерного импульса
много больше длительности лазерного импульса 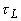 , то диффузией тепла в процессе лазерного нагрева среды можно пренебречь.
, то диффузией тепла в процессе лазерного нагрева среды можно пренебречь.
При поглощении в среде короткого лазерного импульса (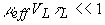 ) интенсивность излучения в среде
) интенсивность излучения в среде 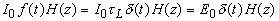 , где
, где 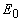 - плотность энергии лазерного излучения на поверхности среды z=0. В этом случае при указанных выше предположениях временная зависимость давления в бегущей акустической волне, излучаемой в поглощающую среду [3,24,40]:
- плотность энергии лазерного излучения на поверхности среды z=0. В этом случае при указанных выше предположениях временная зависимость давления в бегущей акустической волне, излучаемой в поглощающую среду [3,24,40]:
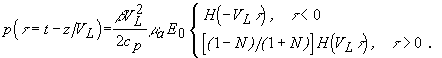 (2.3.1)
(2.3.1)
Здесь
N - отношение акустических импедансов поглощающей и прозрачной сред (для акустически жесткой границы поглощающей среды N = 1, для свободной границы - N >> 1),
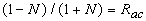 - коэффициент отражения ультразвуковой волны от границы раздела. Таким образом, оптико-акустический (ОА) сигнал (2.3.1) представляет собой волну сжатия и следующую за ней волну разрежения (при N > 1) или сжатия (при N < 1). При малых, но конечных значениях
- коэффициент отражения ультразвуковой волны от границы раздела. Таким образом, оптико-акустический (ОА) сигнал (2.3.1) представляет собой волну сжатия и следующую за ней волну разрежения (при N > 1) или сжатия (при N < 1). При малых, но конечных значениях 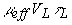
(
£
0.1) переходная зона между фазами имеет длительность порядка 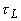 . Общая длительность ОА сигнала определяется временем пробега звука по области тепловыделения и составляет
. Общая длительность ОА сигнала определяется временем пробега звука по области тепловыделения и составляет 
.
Необходимо отметить, что выражение (2.3.1) получено без учета дифракции ОА сигнала при распространении в исследуемой среде. Если регистрация ОА сигнала
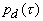 , прошедшего исследуемую среду толщины L, происходит на оси акустического пучка (апертура приемника много меньше радиуса акустического пучка
, прошедшего исследуемую среду толщины L, происходит на оси акустического пучка (апертура приемника много меньше радиуса акустического пучка 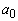 на поверхности среды), то
на поверхности среды), то 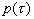 можно восстановить (см. (1.2.17), а также [3,40]).
можно восстановить (см. (1.2.17), а также [3,40]).
Как видно из (2.3.1), передний фронт ОА сигнала
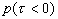 повторяет пространственное распределение интенсивности света в среде, причем временной масштаб изменения p и пространственный масштаб изменения H связаны через скорость звука в среде:
повторяет пространственное распределение интенсивности света в среде, причем временной масштаб изменения p и пространственный масштаб изменения H связаны через скорость звука в среде: 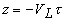 . При прямой регистрации ОА сигналов (в поглощающей среде) [24, 40] момент t
= 0 соответствует приходу на акустический приемник сигнала, возбуждаемого на поверхности исследуемой среды z = 0. При свободной границе поглощающей среды
. При прямой регистрации ОА сигналов (в поглощающей среде) [24, 40] момент t
= 0 соответствует приходу на акустический приемник сигнала, возбуждаемого на поверхности исследуемой среды z = 0. При свободной границе поглощающей среды 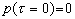 (за счет отражения от границы сигнала в противофазе), а при жесткой границе
(за счет отражения от границы сигнала в противофазе), а при жесткой границе 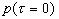 имеет локальный минимум [25,27-29], соответствующий локальному минимуму в распределении
имеет локальный минимум [25,27-29], соответствующий локальному минимуму в распределении 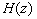 интенсивности света в среде при z=0 (см. выше). Определение момента t
=0 на экспериментально полученном и скорректированном с учетом (2.3.2) временном профиле давления ОА сигнала позволяет преобразовать временную зависимость переднего фронта ОА импульса
интенсивности света в среде при z=0 (см. выше). Определение момента t
=0 на экспериментально полученном и скорректированном с учетом (2.3.2) временном профиле давления ОА сигнала позволяет преобразовать временную зависимость переднего фронта ОА импульса 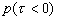 в пространственную зависимость
в пространственную зависимость 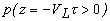 . Эта зависимость, нормированная на
. Эта зависимость, нормированная на 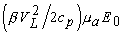 , есть распределение интенсивности света в среде H
, есть распределение интенсивности света в среде H(
z) (см. (2.2.29) и (2.3.1)). Таким образом, оптико-акустический метод дает возможность проводить прямое измерение пространственного распределения интенсивности света в рассеивающей среде, если коэффициент поглощения света, скорость звука и теплофизические параметры среды, а также плотность энергии лазерного излучения на поверхности среды известны.
На расстояниях
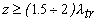
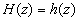 и поэтому (см. (2.2.29) и (2.3.1))
и поэтому (см. (2.2.29) и (2.3.1))

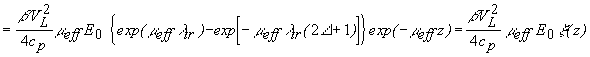 (2.3.3)
(2.3.3)
Поэтому для рассеивающей среды с неизвестными оптическими характеристиками по экспоненциальной зависимости фронта ОА сигнала
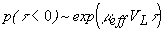 определяется коэффициент экстинкции света
определяется коэффициент экстинкции света 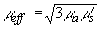 . По абсолютной величине нормированного на
. По абсолютной величине нормированного на 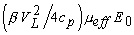 давления ОА сигнала x
давления ОА сигнала x
(
z) в области, где наблюдается его экспоненциальный спад, определяется значение 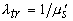 . Зная величины
. Зная величины 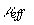 и
и 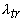 , можно определить
, можно определить 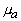 и
и 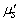
.
Таким образом, по форме переднего фронта давления оптико-акустического сигнала, зарегистрированного с высоким временным разрешением в абсолютных единицах, можно рассчитать оптические характеристики рассеивающей среды - коэффициент поглощения и приведенный коэффициент рассеяния света.
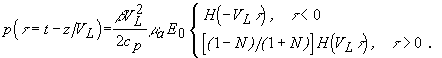 (2.3.1)
(2.3.1)
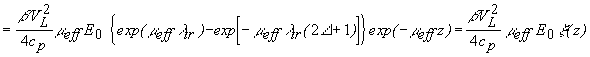 (2.3.3)
(2.3.3)