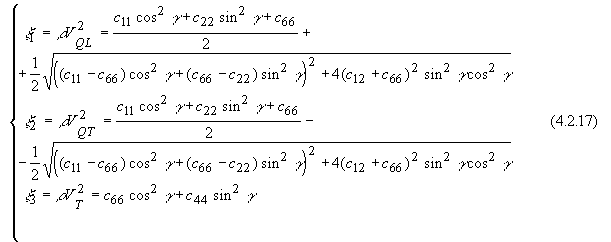|
4.2 Теоретическая модель распространения ультразвука в однонаправленных графито-эпоксидных композитах: длинноволновый случай.
Как было замечено в предыдущем параграфе, неразрушающий контроль композитов, в частности контроль процесса старения, можно осуществить, зная полный набор упругих модулей материала и исследуя изменение модулей в процессе эксплуатации. Однако только для узкого класса композитных материалов возможно измерение матрицы жесткости, что связано со сложным характером анизотропии последних [68,103]. В случае однонаправленных г/э композитов логично предположить, что при распространении упругих волн в длинноволновом случае, вещество будет вести себя как квазиоднородное и трансверсально-изотропное с осью симметрии, определяемой направлением волокон. Измерение полного набора упругих модулей в таком приближении возможно [102,104]. В данном параграфе будут получены формулы [80], позволяющие найти упругие константы трансверсально-изототропных веществ по их плотности и фазовым скоростям, распространяющихся в них УЗ волн. Возмущенное состояние идеально упругой среды характеризуется вектором упругих смещений определяющим отклонение материальной точки среды от положения равновесия (4.2.2) Реакция среды на деформацию описывается тремя координатными векторами напряжений (4.2.3) Вектором Обычно в теории упругости предполагается, что напряжения можно разложить в ряд по степеням деформаций
В линейной теории упругости предполагается, что деформации малы, а разложение (4.2.4) ограничивается только первыми двумя членами (причем tij(0)=0). Тогда связь между напряжениями и деформациями будет выглядеть следующим образом: где
Выражение (4.2.5) представляет собой закон Гука в линейной среде. Коэффициенты cijkl выражают в общем виде линейное соотношение между тензорами второго ранга(11) « 1 (22) « 2 (33) « 3 (23)=(32) « 4 ; Þ сijkl « сa b . (31)=(13) « 5 (12)=(21) « 6. При переходе из одной ортогональной системы координат где по всем повторяющимся индексам идет суммирование. Исходя из симметрии рассматриваемого класса веществ и закона преобразования (4.2.6), непосредственно следует, что ненулевых компонент у матрицы жесткости трансверсально изотропных веществ всего двенадцать: Т.к. ось где Сила, действующая на единичный объем тела, испытывающий внутреннее напряжение tij, равна Используя закон Гука (4.5) , получим уравнение движения в виде [115]: Будем искать решение этого уравнения в виде плоской волны, распространяющейся в направлении, определяемом единичным вектором нормали k где V и e - фазовая скорость и вектор поляризации плоской волны, распространяющейся в направлении k. Тогда получим: Вводя тензор второго ранга Г ilГ il el = r V2 ui(4.2.13)Уравнение (4.2.13) называется уравнением Кристоффеля, которое показывает, что вектор поляризации e является собственным вектором тензора Гil с собственным значениемТаким образом, для определения скорости и поляризации плоских волн, распространяющихся вдоль направления k в анизотропной среде с матрицей жесткости cijkl, нужно найти собственные вектора и собственные значения тензора Гil Так как матрица жесткости cijkl является симметричной, то тензор Гil также будет симметричным, и его собственные значения будут являться действительными величинами, а собственные вектора - ортогональными. Поэтому в анизотропной среде вдоль направления k могут распространяться три плоские волны с различными скоростями и ортогональными поляризациями .Для трансверсально изотропных веществ компоненты тензора Г il будут иметь вид:Г 11 =Г 12 =Г 13 =Г 22 =Г 23 =Г 33 =Выражения (4.2.15) показывают, что варьируя направление распространения УЗ волны в трансверсально изотропном веществе, можно получить искомую связь фазовых скоростей с упругими модулями. Пусть акустическая волна распространяется вдоль оси симметрии Г 11 =Первый корень соответствует соответствует чисто продольной акустической волне; два других - чисто поперечным волнам, распространяющимся вдоль оси Таким образом, можно определить упругие модули Смешанный модуль c12 не удается определить, исследовав распространение акустических волн только вдоль главных осей трансверсально-изотропного вещества. Для его нахождения необходимо рассмотреть распространение УЗ волн в других направлениях (проще всего в плоскости (
Cледовательно, зная фазовые скорости квазипродольной ( QL) и квазипоперечных (QT) волн в плоскости волокон, можно согласно формулам (4.2.17) вычислить недостающий упругий модуль
|
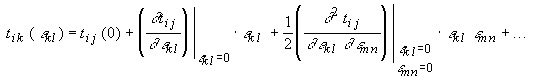 (4.2.4)
(4.2.4)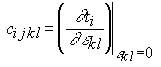 (4.2.5)
(4.2.5)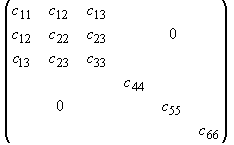 (4.2.7)
(4.2.7)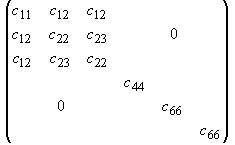 (4.2.8)
(4.2.8)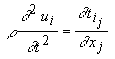 (4.2.9)
(4.2.9)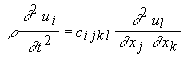 (4.2.10)
(4.2.10)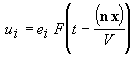 (4.2.11)
(4.2.11)